Abstract
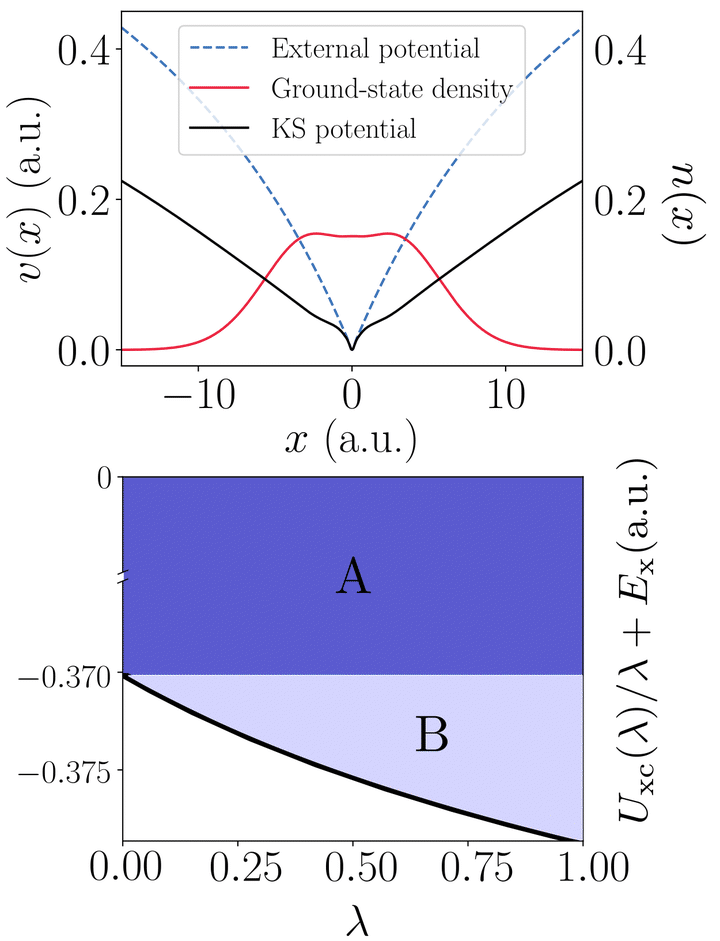
In the context of inhomogeneous one-dimensional finite systems, recent numerical advances [Phys. Rev. B 103, 125155 (2021)] allow us to compute the exact coupling-constant dependent exchange-correlation kernel within linear response time-dependent density functional theory. This permits an improved understanding of ground-state total energies derived from the adiabatic-connection fluctuation-dissipation theorem (ACFDT). We consider both ‘one-shot’ and ‘self-consistent’ ACFDT calculations, and demonstrate that chemical accuracy is reliably preserved when the frequency dependence in the exact functional fxc(w=0) is neglected. This performance is understood on the grounds that the exact fxc varies slowly over the most relevant w range (but not in general), and hence the spatial structure in fxc(w=0) is able to largely remedy the principal issue in the present context: self-interaction (examined from the perspective of the exchange-correlation hole). Moreover, we find that the implicit orbitals contained within a self-consistent ACFDT calculation utilizing the adiabatic exact kernel fxc(w=0) are remarkably similar to the exact Kohn-Sham orbitals, thus further establishing that the majority of the physics required to capture the ground-state total energy resides in the spatial dependence of fxc at w=0.