Abstract
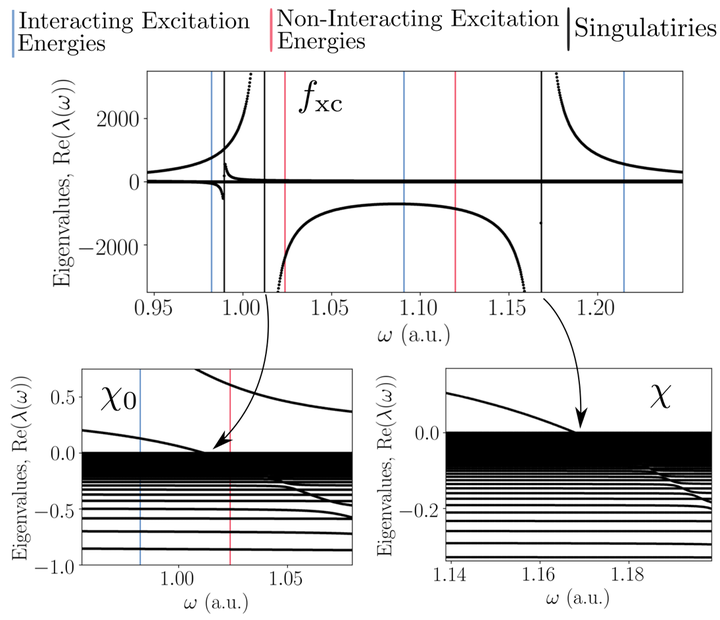
The exact exchange-correlation (xc) kernel fxc(x,x',w) of linear response time-dependent density functional theory is computed over a wide range of frequencies for three canonical one-dimensional finite systems. Methods used to ensure the numerical robustness of fxc are set out. The frequency dependence of fxc is found to be largely due to its analytic structure, i.e., its singularities at certain frequencies, which are required in order to capture particular transitions, including those of double excitation character. However, within the frequency range of the first few interacting excitations, fxc is approximately w independent, meaning the exact adiabatic approximation fxc(w=0) remedies the failings of the local density approximation and random phase approximation for these lowest transitions. The key differences between the exact fxc and its common approximations are analyzed, and cannot be eliminated by exploiting the limited gauge freedom in fxc. The optical spectrum benefits from using as accurate as possible an fxc and ground-state xc potential, while maintaining exact compatibility between the two is of less importance.